Pythonで体験するベイズ推論 PyMCによるMCMC入門 第1章 写経
始めに
この記事では、Pythonで体験するベイズ推論 PyMCによるMCMC入門
の第1章を写経した記録をまとめます。実行はJupyter Labにて実行しています。
写経は以下のようにまとめました。
写経ではありますが、コードを実行しやすいように関数を作成し、コードの再実行がやりやすいようにしてあります。
また、より良いと思われるコードを考えた場合は書き換えてコメントを添えるようにし、変更点をなるべく明示するようにしてあります。
個人的に気になった点のメモを残すようにしてあります。同じような疑問を持った方の助けになれば幸いです。
Pythonで体験するベイズ推論 PyMCによるMCMC入門を読んでいている際のちょっとした正誤表代わりになればと思います。
1.2 ベイズ推論の枠組み
1.2.2 例題:司書か農家か?
メモ
IPython.core.pylabtoolsはIpythonのAPIの一つで、Pylab (matplotlib) の操作をサポートしてくれる関数がまとめられています。インポートしたfigsize関数はデフォルトの画像サイズを設定してくれる関数です。
figsize(12.5, 4)は
matplotlib.rcParams['figure.figsize'] = [25, 8]
を実行することでできるそう。
from IPython.core.pylabtools import figsize import numpy as np from matplotlib import pyplot as plt
%matplotlib inline figsize(25, 8) # テキストの値だと、画像が小さかったので、2倍のサイズを指定した。 plt.rcParams['font.size'] = 25 # フォントのサイズを大きくする。
colors = ["#348ABD", "#A60628"] prior = [1 / 21., 20 / 21.] posterior = [0.087, 1 - 0.087] plt.bar([0, .7], prior, alpha=0.70, width=0.25, color=colors[0], label="prior distribution", lw="3", edgecolor=colors[0]) # テキストでは、edgecolor="#348ABD"と書いてあったが、これはcolors[0]のことなので書き直した。 plt.bar([0 + 0.25, .7 + 0.25], posterior, alpha=0.7, width=0.25, color=colors[1], label="posterior distribution", lw="3", edgecolor=colors[1]) # テキストでは、edgecolor="#A60628"と書いてあったが、これはcolors[1]のことなので書き直した。 plt.xticks([0.20, 0.95], ["Librarian", "Farmer"]) plt.xlabel("Probability") plt.legend(loc="upper left") plt.title("Prior and posterior probabilities of Steve's occupation")
Text(0.5, 1.0, "Prior and posterior probabilities of Steve's occupation")

1.3 確率分布
1.3.1 離散の場合
import scipy.stats as stats
def plot_two_poi_dist(lambda_0=1.5, lambda_1=4.25): poi = stats.poisson colors = ["#348ABD", "#A60628"] a = np.arange(16) plt.bar(a, poi.pmf(a, lambda_0), color=colors[0], label=f"$\lambda = {lambda_0}$", # テキストだと%によりlambda_[0]の値を文字列の中に埋め込んでいたが、fを使えばよいだろう。%を使うことに何か利点があるのかな? alpha=0.6, edgecolor=colors[0], lw=3) #alphaはバーの透明度。0だと透明(見えない)、1だと透過なし。 #lwはエッジの幅のようだ。テキストはなぜか"3"のように文字列を指定していたが、整数を渡せばいいと思う。エラーにならないのは、整数への変換が内部で起っているのかな? plt.bar(a, poi.pmf(a, lambda_1), color=colors[1], label=f"$\lambda = {lambda_1}$", alpha=0.60, edgecolor=colors[1], lw=3) plt.xticks(a + 0.4, a) plt.legend() plt.ylabel("Probability of $k$") plt.xlabel("$k$") plt.title("Probability mass function of a Poisson random variable, differing $\lambda$ values")
plot_two_poi_dist()

メモ
モジュールscipy.statsは種々の確率質量関数と確率密度関数を生成するクラスをまとめたもののようです。
参考:Statistics (scipy.stats)、Statistical functions (scipy.stats)
たとえば、上のコードにあるように
poi = stats.poisson
type(poi)
scipy.stats._discrete_distns.poisson_gen
により作成されたクラスpoisson_genのインスタンスpoiは、メソッドpmfによりポアソン分布の確率質量関数の値を計算することができます。
poi.pmf(3, 4) # 平均が4であるポアソン分布の確率質量関数がx=3においてとる値を計算する。
0.19536681481316454
また、平均や分散も計算してくれるようです。
poi.stats(4)
(array(4.0), array(4.0))
当たり前のように、ポアソン分布に従う確率変数を生成することもできます。メソッドrvsを使います。
poi.rvs(4, size=10)
array([ 7, 7, 5, 1, 10, 7, 4, 8, 1, 6])
ちなみに、平均を指定してインスタンスを作成することができます。
poi_4 = stats.poisson(4)
poi_4.pmf(3)
0.19536681481316454
このようにして作成されたインスタンスはfrozen objectなどと呼ばれるようです。
Alternatively, the distribution object can be called (as a function) to fix the shape and location. This returns a “frozen” RV object holding the given parameters fixed.
平均を指定せずに作成したpoiとは異なるクラスになるようです。
type(poi_4)
scipy.stats._distn_infrastructure.rv_frozen
1.3.2 連続の場合
def plot_two_expo_dist(lambda_=[0.5, 4]): a = np.linspace(0, 4, 100) expo = stats.expon colors = ["#348ABD", "#A60628"] for l, c in zip(lambda_, colors): plt.plot(a, expo.pdf(a, scale=1. / l), lw=3, color=c, label=f"$\lambda = {l}") plt.fill_between(a, expo.pdf(a, scale=1. / l), color=c, alpha=.33) plt.legend() plt.ylabel("Probability density function at $z$") plt.xlabel("$z$") plt.ylim(0, 1.2) plt.title("Probability density function of an exponential " "random variable, differing $\lambda$ values")
plot_two_expo_dist()

メモ
fill_betweenは二つの曲線の間を塗りつぶす関数のようです。
参考:matplotlib.pyplot.fill_between
次の関数のように、二つの曲線(expo.pdf(a, scale=1. / lambda_[0])とexpo.pdf(a, scale=1. / lambda_[1]))を指定すると、その間を塗りつぶしてくれる。
def plot_two_expo_dist2(lambda_=[0.5, 4]): a = np.linspace(0, 4, 100) expo = stats.expon colors = ["#348ABD", "#A60628"] for l, c in zip(lambda_, colors): plt.plot(a, expo.pdf(a, scale=1. / l), lw=3, color=c, label=f"$\lambda = {l}$") plt.fill_between(a, expo.pdf(a, scale=1. / lambda_[0]), expo.pdf(a, scale=1. / lambda_[1]), color="#00d000", alpha=.33) plt.legend() plt.ylabel("Probability density function at $z$") plt.xlabel("$z$") plt.ylim(0, 1.2) plt.title("Probability density function of an exponential " "random variable, differing $\lambda$ values")
plot_two_expo_dist2()

1.4 コンピュータにベイズ推論をさせるには
1.4.1 例題:メッセージ数に変化はあるか?
from os import makedirs makedirs("data", exist_ok=True)
from urllib.request import urlretrieve urlretrieve("https://git.io/vXTVC", "data/txtdata.csv")
('data/txtdata.csv', <http.client.HTTPMessage at 0x2e155deb8d0>)
count_data = np.loadtxt("data/txtdata.csv")
def plot_uss_txt_hab(count_data=count_data): n_count_data = len(count_data) plt.bar(np.arange(n_count_data), count_data, color="#348ABD") plt.xlabel("Time (days)") plt.ylabel("Text messages received") plt.title("Did the user's texting habits change over time?") plt.xlim(0, n_count_data)
plot_uss_txt_hab()

1.4.2 一撃必殺:PyMC
import pymc as pm
alpha = 1.0 / count_data.mean() lambda_1 = pm.Exponential("lambda_1", alpha) lambda_2 = pm.Exponential("lambda_2", alpha) n_count_data = len(count_data) tau = pm.DiscreteUniform("tau", lower=0, upper=n_count_data) print(f"Random output: {tau.random()} {tau.random()} {tau.random()}")
Random output: 10 48 50
@pm.deterministic def lambda_(tau=tau, lambda_1=lambda_1, lambda_2=lambda_2): out = np.zeros(n_count_data) out[:tau] = lambda_1 out[tau:] = lambda_2 return out
observation = pm.Poisson("obs", lambda_, value=count_data, observed=True) model = pm.Model([observation, lambda_1, lambda_2, tau])
mcmc = pm.MCMC(model) mcmc.sample(40000, 10000)
[-----------------100%-----------------] 40000 of 40000 complete in 6.6 sec
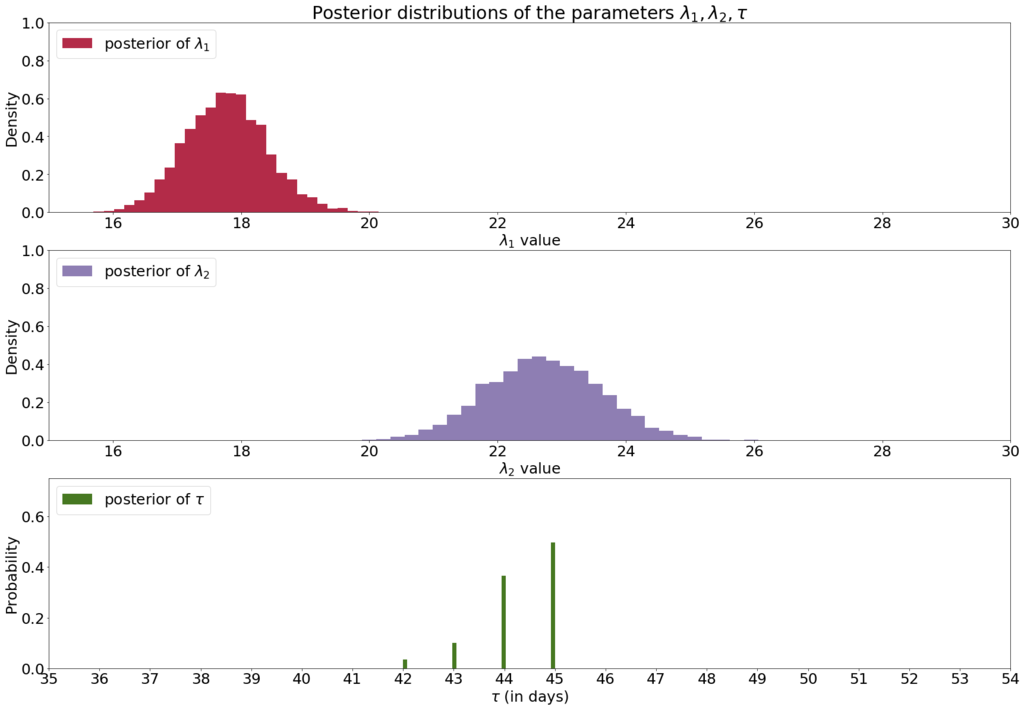
def plot_post_dist(mcmc=mcmc): figsize(29, 20) lambda_1_samples = mcmc.trace('lambda_1')[:] lambda_2_samples = mcmc.trace('lambda_2')[:] tau_samples = mcmc.trace('tau')[:] ax = plt.subplot(311) ax.set_autoscaley_on(False) plt.hist(lambda_1_samples, histtype='stepfilled', bins=30, alpha=0.85, color="#A60628", density=True, # normedという引数はどうやらMatplotlib 3.1では削除されてしまうらしいのでdensityを使用した。 label="posterior of $\lambda_1$") plt.legend(loc="upper left") plt.title("Posterior distributions of the parameters " r"$\lambda_1, \lambda_2, \tau$") plt.xlim([15, 30]) plt.xlabel("$\lambda_1$ value") plt.ylabel("Density") ax = plt.subplot(312) ax.set_autoscaley_on(False) plt.hist(lambda_2_samples, histtype='stepfilled', bins=30, alpha=0.85, color="#7A68A6", density=True, # normedという引数はどうやらMatplotlib 3.1では削除されてしまうらしいのでdensityを使用した。 label="posterior of $\lambda_2$") plt.legend(loc="upper left") plt.xlim([15, 30]) plt.xlabel("$\lambda_2$ value") plt.ylabel("Density") plt.subplot(313) w = 1.0 / tau_samples.shape[0] * np.ones_like(tau_samples) plt.hist(tau_samples, bins=n_count_data, alpha=1, label=r"posterior of $\tau$", color="#467821", weights=w, rwidth=2.) plt.xticks(np.arange(n_count_data)) plt.legend(loc="upper left") plt.ylim([0, .75]) plt.xlim([35, len(count_data) - 20]) plt.xlabel(r"$\tau$ (in days)") plt.ylabel("Probability")
plot_post_dist()
def plot_expc_txt(mcmc=mcmc, count_data=count_data, n_count_data=n_count_data): figsize(25, 8) lambda_1_samples = mcmc.trace('lambda_1')[:] lambda_2_samples = mcmc.trace('lambda_2')[:] tau_samples = mcmc.trace('tau')[:] N = tau_samples.shape[0] expected_texts_per_day = np.zeros(n_count_data) for day in range(n_count_data): ix = day < tau_samples expected_texts_per_day[day] = (lambda_1_samples[ix].sum() + lambda_2_samples[~ix].sum()) / N plt.plot(range(n_count_data), expected_texts_per_day, lw=4, color="#E24A33", label="Expected number of text messages received") plt.xlim(0, n_count_data) plt.ylim(0, 60) plt.xlabel("Day") plt.ylabel("Number of text messages") plt.title("Number of text messages received versus expected number received") plt.bar(np.arange(len(count_data)), count_data, color="#348ABD", alpha=0.65, label="Observed text messages per day") plt.legend(loc="upper left") print(expected_texts_per_day)
plot_expc_txt()
[ 17.76436598 17.76436598 17.76436598 17.76436598 17.76436598
17.76436598 17.76436598 17.76436598 17.76436598 17.76436598
17.76436598 17.76436598 17.76436598 17.76436598 17.76436598
17.76436598 17.76436598 17.76436598 17.76436598 17.76436598
17.76436598 17.76436598 17.76436598 17.76436598 17.76436598
17.76436598 17.76436598 17.76436598 17.76436598 17.76436598
17.76436598 17.76436598 17.76436598 17.76436598 17.76436598
17.76436598 17.76436598 17.76436598 17.76436598 17.76451967
17.76484233 17.7669707 17.91943442 18.38499061 20.19507103
22.72249711 22.72249711 22.72249711 22.72249711 22.72249711
22.72249711 22.72249711 22.72249711 22.72249711 22.72249711
22.72249711 22.72249711 22.72249711 22.72249711 22.72249711
22.72249711 22.72249711 22.72249711 22.72249711 22.72249711
22.72249711 22.72249711 22.72249711 22.72249711 22.72249711
22.72249711 22.72249711 22.72249711 22.72249711]

1.5 おわりに
付録
実際に二つのλは異なっているのか?
lambda_1_samples = mcmc.trace('lambda_1')[:] lambda_2_samples = mcmc.trace('lambda_2')[:] tau_samples = mcmc.trace('tau')[:]
print(lambda_1_samples < lambda_2_samples)
[ True True True ..., True True True]
print((lambda_1_samples < lambda_2_samples).sum()) print(lambda_1_samples.shape[0])
30000
30000
どうやら、僕がやったシミュレーションではlambda_2_samplesの全ての要素がlambda_1_samplesの全ての要素より大きかったようです。もちろん確率も1。
print((lambda_1_samples < lambda_2_samples).mean())
1.0
for d in [1, 2, 5, 10]: v = (abs(lambda_1_samples - lambda_2_samples) >= d).mean() print(f"What is the probability the difference is larger than {d}? {round(v, 2)}")
What is the probability the difference is larger than 1? 1.0
What is the probability the difference is larger than 2? 1.0
What is the probability the difference is larger than 5? 0.49
What is the probability the difference is larger than 10? 0.0
二つの変化点への拡張
def plot_post_dist(count_data=count_data): figsize(29, 20) alpha = 1.0 / count_data.mean() lambda_1 = pm.Exponential("lambda_1", alpha) lambda_2 = pm.Exponential("lambda_2", alpha) lambda_3 = pm.Exponential("lambda_3", alpha) n_count_data = len(count_data) tau_1 = pm.DiscreteUniform("tau_1", lower=0, upper=n_count_data - 1) tau_2 = pm.DiscreteUniform("tau_2", lower=tau_1, upper=n_count_data) @pm.deterministic def lambda_(tau_1=tau_1, tau_2=tau_2, lambda_1=lambda_1, lambda_2=lambda_2, lambda_3=lambda_3): out = np.zeros(n_count_data) out[:tau_1] = lambda_1 out[tau_1:tau_2] = lambda_2 out[tau_2:] = lambda_3 return out observation = pm.Poisson("obs", lambda_, value=count_data, observed=True) model = pm.Model([observation, lambda_1, lambda_2, lambda_3, tau_1, tau_2]) mcmc = pm.MCMC(model) mcmc.sample(40000, 10000) lambda_1_samples = mcmc.trace('lambda_1')[:] lambda_2_samples = mcmc.trace('lambda_2')[:] lambda_3_samples = mcmc.trace('lambda_3')[:] tau1_samples = mcmc.trace('tau_1')[:] tau2_samples = mcmc.trace('tau_2')[:] # lambda_達をプロットするときにxlimを設定するのに使う lambda_min = min([min(lambda_1_samples), min(lambda_2_samples), min(lambda_3_samples)]) lambda_max = max([max(lambda_1_samples), max(lambda_2_samples), max(lambda_3_samples)]) ax = plt.subplot(511) ax.set_autoscaley_on(False) plt.hist(lambda_1_samples, histtype='stepfilled', bins=30, alpha=0.85, color="#A60628", density=True, # normedという引数はどうやらMatplotlib 3.1では削除されてしまうらしいのでdensityを使用した。 label="posterior of $\lambda_1$") plt.legend(loc="upper left") plt.title("Posterior distributions of the five unknown " "parameters in the extended text-message model") plt.xlim([lambda_min - 1, lambda_max + 1]) plt.xlabel("$\lambda_1$ value") plt.ylabel("Density") plt.subplot(512) ax.set_autoscaley_on(False) plt.hist(lambda_2_samples, histtype='stepfilled', bins=30, alpha=0.85, color="#7A68A6", density=True, # normedという引数はどうやらMatplotlib 3.1では削除されてしまうらしいのでdensityを使用した。 label="posterior of $\lambda_2$") plt.legend(loc="upper left") plt.xlim([lambda_min - 1, lambda_max + 1]) plt.xlabel("$\lambda_2$ value") plt.ylabel("Density") ax = plt.subplot(513) ax.set_autoscaley_on(False) plt.hist(lambda_3_samples, histtype='stepfilled', bins=30, alpha=0.85, color="#7A68A6", density=True, # normedという引数はどうやらMatplotlib 3.1では削除されてしまうらしいのでdensityを使用した。 label="posterior of $\lambda_3$") plt.legend(loc="upper left") plt.xlim([lambda_min - 1, lambda_max + 1]) plt.xlabel("$\lambda_3$ value") plt.ylabel("Density") ax = plt.subplot(514) w = 1.0 / tau1_samples.shape[0] * np.ones_like(tau1_samples) plt.hist(tau1_samples, bins=n_count_data, alpha=1, label=r"posterior of $\tau_1$", color="#467821", weights=w, rwidth=2.) plt.xticks(np.arange(n_count_data)) plt.legend(loc="upper left") plt.ylim([0, .75]) plt.xlim([min(tau1_samples) - 1, max(tau2_samples) + 1]) # テキストだと、35日目から54日目までを固定してプロットしてるが、 #これだとmcmc.sampleの結果によっては範囲外にプロットされてしまうのでこのように書き換えた。 plt.xlabel("Day") plt.ylabel("Probability") ax = plt.subplot(515) w = 1.0 / tau2_samples.shape[0] * np.ones_like(tau2_samples) plt.hist(tau2_samples, bins=n_count_data, alpha=1, label=r"posterior of $\tau_2$", color="#467821", weights=w, rwidth=2.) plt.xticks(np.arange(n_count_data)) plt.legend(loc="upper left") plt.ylim([0, .75]) plt.xlim([min(tau1_samples) - 1, max(tau2_samples) + 1]) # テキストだと、35日目から54日目までを固定してプロットしてるが、 #これだとmcmc.sampleの結果によっては範囲外にプロットされてしまうのでこのように書き換えた。 plt.xlabel("Day") plt.ylabel("Probability")
mcmc.sample(40000, 10000)の結果によっては、テキストの結果と大分違う場合があるようです。
plot_post_dist()
[-----------------100%-----------------] 40000 of 40000 complete in 10.1 sec

plot_post_dist()
[-----------------100%-----------------] 40000 of 40000 complete in 14.5 sec

plot_post_dist()
[-----------------100%-----------------] 40000 of 40000 complete in 10.1 sec

今回の写経は以上です。 ここまで読んでいただきありがとうございました。
